Съобщения в телекомуникациите
1. Видове съобщения
Информацията се обменя чрез съобщения.
Съобщенията a(t) са дискретни и аналогови.
Дискретни са тези съобщения, които се изграждат от краен брой символи. Такива са съобщенията в телеграфията, при предаване на данни, в телемеханиката, при комуникация между компютрите и т.н. Броят на символите зависи от азбуката или бройната система, която се използва.
Аналогови (непрекъснати) се наричат съобщенията, съставени от неограничен брой символи, т.е. използващи неограничено голяма азбука. Те се представят чрез непрекъсната функция на времето. Типично аналогови са звуковите съобщения, в които се използват безкрайно много стойности на тоновете и силата на звука, но в зададен интервал на изменение.
2 Параметри на съобщенията
Основните параметри на съобщението са информационните. Те са:
- количество информация, която се съдържа в съобщението;
- информационна производителност и капацитетът на източника;
- информационен излишък на съобщението.
1. Количество информация
За да се разбере, как се определя количеството информация, трябва да се припомни понятието ентропия.
Ентропията H(а) (entropy) е мярка за неопределеност. Ако е известно всичко за нещото, ентропията му има стойност нула. Когато нищо не е известно, ентропията му е безкрайност.
Информацията Ia, която се получава със съобщението, «погасява» неопределеността. В съобщението аi се съдържа информация Ia, която е разликата между стойностите на ентропията преди H1(аi) и след получаване на съобщението от получателя H2(аi):
(2.1) Ia = H1(аi) - H2(аi)
Съвкупността на всички възможни съобщения за «нещото» и тяхната вероятност за поява образува ансамбъл от съобщения. Най-простият ансамбъл се състои от две съобщения а1 и а2, напр. а1 – «Сега е ден», а2 – «Сега е нощ». Могат да бъдат и а1 = 1 и а2 = 0, «ези»/«тура», + /−, «добро»/«лошо» и пр.
Мярката за количество информация е логаритмична: -log2P(а), където P е вероятността да се получи съобщение а. Тъй като вероятността е по-малка от и най-много равна на 1, пред логаритъма има отрицателен знак – за да се получи количеството в положителни числа. Да поясним това за най-простия ансамбъл.
Нека съобщенията са независими и равновероятни, т.е. вероятността Р(а1) да се получи съобщение а1 да е равна на вероятността Р(а2) да се получи съобщение а2: Р(а1) = Р(а2) = Р(а) = ½. При приемане на съобщение а е дошла информация, чието количество е:
(2.2) 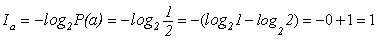
Това е най-малкото цяло число, с което се измерва количество информация, наречено "binary digit" съкратено 1 bit. Ако едното от съобщенията а1 и а2 е по-вероятно от другото, информацията щеше да е по-малко от 1 bit.
Преди да хвърлим една монета не знаем какво ще се падне – ези или тура, но знаем, че вероятността за всяка от двете възможности а1 и а2 е равна, т.е. Р1(а1) = Р2(а2) = 0,5. По формула (2.2) може да се намери: 
След падането на монетата е получен един бит информация. Същата информация се получава и при пренасяне на съобщение с електрически импулс, който има две равновероятни стойности 1 и 0, ако са с еднаква вероятност.
В общия случай при n равновероятни съобщения в ансамбъла количеството информация, която носи всяко от тях е:
(2.3) 
Благодарение на логаритмичната мярка количеството информация , съдържащо се в няколко независими съобщения  , се получава равно на сумата от информацията, съдържаща се във всяко от тях:
, се получава равно на сумата от информацията, съдържаща се във всяко от тях:
(2.4) 
Това съответства на интуитивната представа за натрупване (събиране) на информацията при получаване на допълнителни сведения и съобщения.
Нека вземем примери:
- Ако хвърлим един зар, вероятността да се падне, примерно, числото 5, е 1/6. За коя да е от шестте страни на куба това е равновероятно. Информацията, която носи съобщението, е:
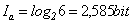
- Да определим количеството информация, което се съдържа в дума, състояща се от 6 букви от руската азбука, където общият брои на буквите е 32. Ще приемем, че вероятността им за поява в съобщението е еднаква и следователно равна на Р(а) = 1/32. Като се замести в (2.3) ще се получи, че всяка буква носи: Iа=log232=5 bit информация. По (2.4) излиза, че количеството информация в думата е
 =6x5=30 bit.
=6x5=30 bit.
Примерът с азбуката обаче не е коректен. Буквите не идват в съобщението с еднаква вероятност. Гласната е се среща много по-често от ъ, съгласната б е по-вероятна от ь и т.н. Тогава не всички съобщения от ансамбъла носят еднаква информация.
В общия случай съобщенията имат различна вероятност за поява. Затова, когато се оценяват като цяло информационните свойства на източника на съобщенията аi ( ) трябва да се определи
) трябва да се определи
ентропията му Н(а). Намира се като сума от количеството информация, която носят всички съобщения, но като се отчита вероятността за поява на всяко съобщение:
(2.5) 
От тази по-обща формула лесно се получават (2.2) и (2.3).
Тази формула е валидна за независими съобщения. Има формули за определяне на ентропията и при зависими съобщения, които тук няма да привеждаме.
Смущенията в комуникационната система променят приетото съобщение. Съобщенията със смущения съдържат по-малко количество информация. Влиянието на смущенията върху ентропията на съобщенията може да се отчете аналитично, ако се знаят неговите количествени параметри.
2. Информационна производителност на източника Ht (bit/s)
Информационна производителност е скоростта на възникване на съобщенията, т.е., количеството информация, съдържаща се в съобщенията за единица време.
Максималната производителност на източника на информация Ht max (bit/s) се нарича капацитет на източника Cи. Очевидно, капацитетът на един морзов апарат е на порядъци по-малка от тази на един компютър, работещ в Internet. Хората говорят различно бързо и имат различен капацитет като източници на информация.
3. Информационен излишък
Най-голяма (Нmax) е ентропията на източника при равновероятна поява на символите в съобщенията от един ансамбъл. Ако възможните съобщения са две, то Нmax = ½.
В общия случай обаче вероятностите не са еднакви, поради което реалната му ентропия е по-малка:
H < Hmax.
Нека в ансамбъла са възможни две съобщения с различна неопределеност H. Напр. два пъти по по-вероятно е да получим положителна новина
Информационният излишък R оценява разликата между реалния случай H и случая, когато съобщенията са равновероятни Hmax, т.е. относителната недонатовареност на съобщенията с информация
(2.6) 

Излишъкът е 50%.
Установено е, че за говоримите езици, включително българския, излишъкът R=70%. Той се е получил в естествените езици при тяхната еволюция, за да осигури разбираемост при наличие на шумове. И да не разберете добре една дума с голяма вероятност можете, благодарение на излишъка, да предполагате, коя е думата. Ако чуете "информация" вярното сигурно е "информация", ако е получено "грешк", можете да го приемете за “грешка” или “грешки” в зависимост от контекста.
Излишъкът, както ще се види по-нататък, служи да защитава достоверността на предаваната информация.
При предаване на данни символите, които ги носят, не се свързват в думи, нямат контекст. Цифрите са равновероятни и нямат излишък, поради което са твърде уязвими от смущения. За откриване и корекция на грешки в приетите съобщения, излишъкът се въвежда изкуствено.
Коментари: